inventory optimization w/ deep q-learning
Inventory Optimization
Major inventory control policies adopted in the supply chain industry nowadays are classic static policies. A dynamic policy that can adaptively adjust the decisions of when and how much to order based on the inventory position and future demand information would be advantageous.
Classic Inventory Control Policies
- (R,Q) Policy : R is reorder point and Q is fixed quantity of ordered product. When inventory drops below R Units, order a fixed quantity of Q units.
- (T,S) Policy: Replenish to S product units every T days, T being the review period and S as the order-up-to level.
- (R,S) Policy: When inventory drops below R Units, place an order to replenish the inventory up to S units.
- (S-1,S) policy: If there is any demand consuming the inventory on a particular day, replenish the inventory up to S units immediately.
The four different policies metnioned above are suitable for different demand patterns, but the similarity is that they all assume either a fixed reorder point, fixed order quantity, fixed order-up-to level or fixed time interval between two orders. Moreover, most of these policies only relies on the current inventory position to make ordering decisions, and does not utilize other possible information related to future demand to help make more informed decisions.
This limits the flexibility of the policy, which potentially undermines the responsiveness of the policy to high demand (causing lost sales) or results in excessive inventory when demand is low (causing inventory holding costs). Can we do better if we remove said limitation? Is tehre a way to build a model to obtain an inventory control policy without this limitation?
In this project, we will try to do this with reinforcement learning (RL).
Reinforcement Learning for Inventory Optimization
Formulating the Markov Decision Process (MDP)
4 elements of MDP:
- State (S_t) -> The situation of the agent at time t
- Action (A_t) -> The decision the agent takes at time t
- Reward (R_t) -> Feedback from the environment towards the agent’s action at time t
-
Transition Probability (S_(t+1) S_t, A_t) -> Probability the state becomes S_(t+1) after taking a specific action A_t in the state S_t
The inventory optimization problem naturally fits the framework of MDP due to its sequential decision making structure.
The next step is to formulate a mathematical model for the problem,
Target Function: Maximizing the profit gotten form selling Coke within a period of time
Parameters:
- Inventory holding cost
- Fixed ordering cost (e.g. Shipping cost)
- Variable ordering cost ( e.g. Price of buying from supplier)
Assumptions:
- No backorder cost, assuming when there is no coke inside the store then customers would just go to another store without placing an order for the future
- Customer demand follows a mixture of normal distributions: Monday to Thursday with the lowest mean, Friday with medium mean, and Saturday to Sunday with the highest mean
RL Definitions
We need to construct the mathematical definitions for the state, action, and reward.
State -> (I_pt, DoW_t), where I_pt is the inventory position (Inventory on-hand + up-coming order) at the end of t-th day, and DoW_t is a 6-dimensional one-hot encoding form of identifying the day of week in which the state is in. This way, the ordering decisions can be made based on the information of which day of the week it is in.
Action -> (A_t), where A_t denotes the order quantity being released at the end of t-th day, the action space is limited by the maximum order quantity determined by suppliers or transportation capacity
Reward -> (R_t) = (min(D_t, I_t) * P) - (I_t * H) - (I(A_t > 0) * F) - (A_t * V), with the definitions being
- D_t is the demand that occurs during the daytime of the (t+1)-th day,
- I_t is the inventory on-hand at the end of t-th day,
- P is the selling price per product unit,
- H is the holding cost per inventory on-hand per night,
- I(A_t > 0) is an indicator function that takes 1 if (A_t > 0) and 0 otherwise,
- F is the fixed ordering cost incurred per order, and
- V is the variable ordering cost per unit.
Solving the MDP
From the case above, the transition probability (P_t) is unknown. In real cases, one could choose to fit a demand distribution using historical demand data, try to infer the transition probabilities and then use a model-based RL technique to solve this problem.
However, this could result in a huge gap between the simulated environment and real world as fitting a perfect demand distribution is very challenging (especially in this case where demand follows a mixture of distributions). Hence, it would be better to adopt model-free RL techniques that can deal with unknown transition probabilities inherently.
There are multiple model-free RL techniques for solving this MDP. In this article, as a first attempt, I adopted Deep Q Network (DQN) as the solving tool. DQN is a variant of Q learning, which utilizes deep neural networks to build an approximation of Q functions. To save on space, I’m omitting the detailed instruction of DQN as it’s not the focus of this article. Interested readers are referred to this article.
The Case
Assume there is a small retail store which sells Coke to its customers. Every time the store wants to replenish its inventory to fulfill customer demand, the store has to place an order of an integer number of cases of Coke (one case contains 24 cans). Suppose that the unit selling price of Coke is 30 dollars per case, holding cost is 3 dollars per case per night, fixed ordering cost is 50 dollars per order, variable ordering cost is 10 dollars per case, the inventory capacity of the store is 50 cases, the maximum order quantity allowed is 20 cases per order, the initial inventory is 25 cases at the end of a Sunday, and the lead time (time interval between placing an order and order arrival) is 2 days. Here, we assume the demand from Monday to Thursday follows a normal distribution N(3,1.5), the demand on Friday follows a normal distribution N(6,1), and the demand from Saturday to Sunday follows a normal distribution N(12,2). We generate 52 weeks of historical demand samples from this mixture of distributions, and use this as a training dataset for the DQN model.
Summary:
- 1 case = 24 cans of Coke
- Unit selling price (P) = 30 dollars per case
- Holding cost (H) = 3 dollars per case
- Fixed ordering cost (F) = 50 dollars per order
- Variable ordering cost (V) = 10 dollars per case
- Maximum inventory capacity (C) = 50 cases
- Maximum order quantity = 20 cases per order
- Initial inventory on-hand (I_0) = 25 cases at the end of Sunday
- Lead time (L) (Time between releasing an order and receiving said order) = 2 days
- The demand follows a normal distribution N(miu, sigma) with miu the mean and sigma being the standard deviation of the demand. Demand from Monday to Thursday follows a normal distribution N(3,1.5), the demand on Friday follows a normal distribution N(6,1), and the demand from Saturday to Sunday follows a normal distribution N(12,2)
- We generate 52 weeks of historical demand samples for training the DQN Model
As a benchmark, we will optimize a classic (s,S) inventory control policy using the same dataset which was used for training the DQN model, and compare its performance with DQN in a test set.
# Data Generation
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
def generate_demand(mean, stdev):
"""
:param mean: mean of the normal distribution
:param stdev: standard deviation of the normal distribution
:return: demand value
"""
random_demand = np.random.normal(mean, stdev)
if random_demand < 0:
random_demand = 0
random_demand = np.round(random_demand)
return random_demand
demand_hist = [] # List of demand data in the past year
for i in range(52): # 52 weeks in a year
for j in range(4): # Data for monday through thursday
random_demand = generate_demand(3,1.5)
demand_hist.append(random_demand)
random_demand = generate_demand(6,1) # Data for friday
demand_hist.append(random_demand)
for j in range(2): # Data for saturday and sunday
random_demand = generate_demand(12,2)
demand_hist.append(random_demand)
print(demand_hist)
plt.hist(demand_hist)
Inventory Optimization Environment
class InvOptEnv():
def __init__(self, demand_records):
self.n_period = len(demand_records) # Number of periods
self.current_period = 1 # Intialized on Monday
self.day_of_week = 0 # Intialized on Monday
self.inv_level = 25 # Initial I_t (I_0)
self.inv_pos = 25 # Initial I_pt (I_0)
self.capacity = 50 # C value
self.holding_cost = 3 # H value
self.unit_price = 30 # P value
self.fixed_order_cost = 50 # F value
self.variable_order_cost = 10 # V value
self.lead_time = 2 # L value
self.order_arrival_list = [] # List of orders that are arriving in the future
self.demand_list = demand_records # List of demand data
self.state = np.array([self.inv_pos] + convert_day_of_week(self.day_of_week)) # State vector
self.state_list = [] # List of state vectors
self.state_list.append(self.state) # Add the initial state vector to the list
self.action_list = [] # List of actions
self.reward_list = [] # List of rewards
def reset(self): # Reset the environment
self.state_list = [] # Reset the state list
self.action_list = [] # Reset the action list
self.reward_list = [] # Reset the reward list
self.inv_level = 25 # Reset the inventory level
self.inv_pos = 25 # Reset the inventory position
self.current_period = 1 # Reset the current period
self.day_of_week = 0 # Reset the day of week
self.state = np.array([self.inv_pos] + convert_day_of_week(self.day_of_week)) # Reset the state vector
self.state_list.append(self.state) # Add the initial state vector to the list
self.order_arrival_list = [] # Reset the order arrival list
return self.state
def step(self, action): # Take an action
if action > 0: # If the action is to order
y = 1
self.order_arrival_list.append([self.current_period+self.lead_time, action]) # Add the order to the list
else: # If the action is not to order
y = 0
if len(self.order_arrival_list) > 0: # If there is an order in the list
if self.current_period == self.order_arrival_list[0][0]: # If the order arrives
self.inv_level = min(self.capacity, self.inv_level + self.order_arrival_list[0][1]) # Update the inventory level
self.order_arrival_list.pop(0) # Remove the order from the list
demand = self.demand_list[self.current_period-1] # Get the demand of the current period
units_sold = demand if demand <= self.inv_level else self.inv_level # Calculate the number of units sold
reward = (units_sold * self.unit_price) - (self.inv_level * self.holding_cost) \
- (y * self.fixed_order_cost) - (action * self.variable_order_cost) # Calculate the reward
self.inv_level = self.inv_level - units_sold # Update the inventory level
self.inv_pos = self.inv_level # Update the inventory position
if len(self.order_arrival_list) > 0: # If there is an order in the list
for i in range(len(self.order_arrival_list)): # For each order in the list
self.inv_pos += self.order_arrival_list[i][1] # Update the inventory position
self.day_of_week = (self.day_of_week + 1) % 7 # Update the day of week
self.state = np.array([self.inv_pos] + convert_day_of_week(self.day_of_week)) # Update the state vector
self.state_list.append(self.state) # Add the state vector to the list
self.action_list.append(action) # Add the action to the list
self.reward_list.append(reward) # Add the reward to the list
self.current_period += 1 # Update the current period
if self.current_period > self.n_period: # If the current period exceeds the total number of periods
done = True # Done
else:
done = False # Not done
return self.state, reward, done
def convert_day_of_week(d):
if d == 0: # Monday
return [0, 0, 0, 0, 0, 0]
if d == 1:
return [1, 0, 0, 0, 0, 0]
if d == 2:
return [0, 1, 0, 0, 0, 0]
if d == 3:
return [0, 0, 1, 0, 0, 0]
if d == 4:
return [0, 0, 0, 1, 0, 0]
if d == 5:
return [0, 0, 0, 0, 1, 0]
if d == 6:
return [0, 0, 0, 0, 0, 1]
import torch.nn as nn
class DQN(nn.Module):
"""
Actor (Policy) Model
"""
def __init__(self, state_dim, action_dim, seed, fc1_dim, fc2_dim):
"""
Initialize parameters and build model.
=======
:param state_dim: state dimension
:param action_dim: action dimension
:param fc1_dim: first fully connected layer dimension
:param fc2_dim: second fully connected layer dimension
"""
super(DQN, self).__init__() # Inherit from the nn.Module class
self.seed = torch.manual_seed(seed) # Set the seed
self.fc1 = nn.Linear(state_dim, fc1_dim)
self.fc2 = nn.Linear(fc1_dim, fc2_dim)
self.fc3 = nn.Linear(fc2_dim, action_dim)
def forward(self, x):
"""
Build a forward pass of the network from state -> action
:param x: state vector
:return: final output
"""
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
out = self.fc3(x)
return out
import random
from collections import namedtuple, deque
import torch
import torch.nn.functional as F
import torch.optim as optim
BUFFER_SIZE = int(5*1e5) # replay buffer size
BATCH_SIZE = 128 # minibatch size
GAMMA = 0.99 # discount factor
TAU = 1e-3 # for soft update of target parameters
LR = 1e-4 # learning rate
UPDATE_EVERY = 4 # how often to update the network
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # Use GPU if available
class Agent():
"""
Interacts with and learns from the environment.
"""
def __init__(self, state_dim, action_dim, seed):
"""
Initialize an Agent object.
Params
======
state_dim (int): dimension of each state
action_dim (int): dimension of each action
seed (int): random seed
"""
self.state_dim = state_dim
self.action_dim = action_dim
self.seed = random.seed(seed)
# DQN initialization
self.dqn_local = DQN(state_dim, action_dim, seed, 128, 128).to(device) # What does local DQN mean? -> The DQN that is being trained
self.dqn_target = DQN(state_dim, action_dim, seed, 128, 128).to(device) # What does target DQN mean? -> The DQN that is being used to predict the Q values
self.optimizer = optim.Adam(self.dqn_local.parameters(), lr=LR)
self.memory = ReplayBuffer(action_dim, BUFFER_SIZE, BATCH_SIZE, seed)
self.t_step = 0 # Initialize time step (for updating every UPDATE_EVERY step)
print("Agent seed:", self.seed)
def step(self, state, action, reward, next_step, done):
"""
Save experience in replay memory, and use random sample from buffer to learn.
:param state: state vector
:param action: action vector
:param reward: reward vector
:param next_step: next state vector
:param done: done vector
:return: None
"""
# Save experience in replay memory
self.memory.add(state, action, reward, next_step, done)
# Learn every UPDATE_EVERY time steps.
self.t_step = (self.t_step + 1) % UPDATE_EVERY
if self.t_step == 0: # If it's time to learn
# If enough samples are available in memory, get random subset and learn
if len(self.memory) > BATCH_SIZE:
experiences = self.memory.sample() # Sample from the replay buffer
self.learn(experiences, GAMMA) # Learn from the sampled experiences
def act(self, state, eps=0.):
"""
Returns actions for given state as per current policy.
:param state: current state
:param eps: epsilon, for epsilon-greedy action selection
:return: action vector
"""
state = torch.from_numpy(state).float().unsqueeze(0).to(device) # Convert the state vector to a torch tensor
self.dqn_local.eval() # Set the local DQN to evaluation mode
with torch.no_grad(): # Disable gradient calculation
action_values = self.dqn_local(state) # Get the action values
self.dqn_local.train() # Set the local DQN to training mode
# Epsilon-greedy action selection
if random.random() > eps: # If the random number is greater than epsilon
return np.argmax(action_values.cpu().data.numpy()) # Return the action with the highest action value
else:
return random.choice(np.arange(self.action_dim)) # Return a random action
def learn(self, experiences, gamma):
"""
Update value parameters using given batch of experience tuples.
:param self:
:param experiences: (Tuple[torch.Variable]): tuple of (s, a, r, s', done) tuples
:param gamma: discount factor
:return:
"""
states, actions, rewards, next_states, dones = experiences # Unpack the experiences
## Compute and minimize the loss
criterion = torch.nn.MSELoss() # Define the loss function
self.dqn_local.train() # Set the local DQN to training mode
self.dqn_target.eval() # Set the target DQN to evaluation mode
# Get the predicted Q values from the local DQN
predicted_targets = self.dqn_local(states).gather(1, actions)
with torch.no_grad(): # Disable gradient calculation
# Get the target Q values from the target DQN
labels_next = rewards + (gamma * self.dqn_target(next_states).detach().max(dim=1)[0].unsqueeze(1))
# .detach() -> Returns a new Tensor, detached from the current graph.
labels = rewards + (gamma * labels_next * (1-dones)) # Calculate the labels
loss = criterion(predicted_targets, labels).to(device) # Calculate the loss
self.optimizer.zero_grad() # Zero the gradients
loss.backward() # Backpropagate
self.optimizer.step() # Update the weights
# ------------------- update target network ------------------- #
self.soft_update(self.dqn_local, self.dqn_target, TAU) # Soft update the target DQN
def soft_update(self, local_model, target_model, tau):
"""
Soft update model parameters.
θ_target = τ*θ_local + (1 - τ)*θ_target
:param local_model: weights will be copied from
:param target_model: weights will be copied to
:param tau: interpolation parameter
:return: None
"""
for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
target_param.data.copy_(tau*local_param.data + (1.0-tau)*target_param.data)
class ReplayBuffer:
def __init__(self, action_dim, buffer_size, batch_size, seed):
"""
Initialize a ReplayBuffer object.
:param action_dim: action dimension
:param buffer_size: maximum size of buffer
:param batch_size: size of each training batch
:param seed: random seed
"""
self.action_dim = action_dim
self.memory = deque(maxlen=buffer_size) # Initialize the replay buffer
self.batch_size = batch_size
self.experience = namedtuple("Experience", field_names=["state",
"action",
"reward",
"next_state",
"done"])
self.seed = random.seed(seed)
print("ReplayBuffer seed:", self.seed)
def add(self, state, action, reward, next_state, done):
"""
Add a new experience to memory.
"""
e = self.experience(state, action, reward, next_state, done)
self.memory.append(e)
def sample(self):
"""
Randomly sample a batch of experiences from memory.
"""
experiences = random.sample(self.memory, k=self.batch_size)
states = torch.from_numpy(np.vstack([e.state for e in experiences if e is not None])).float().to(device)
actions = torch.from_numpy(np.vstack([e.action for e in experiences if e is not None])).long().to(device)
rewards = torch.from_numpy(np.vstack([e.reward for e in experiences if e is not None])).float().to(device)
next_states = torch.from_numpy(np.vstack([e.next_state for e in experiences if e is not None])).float().to(device)
dones = torch.from_numpy(np.vstack([e.done for e in experiences if e is not None]).astype(np.uint8)).float().to(device)
return (states, actions, rewards, next_states, dones)
def __len__(self):
"""
Return the current size of internal memory.
"""
return len(self.memory)
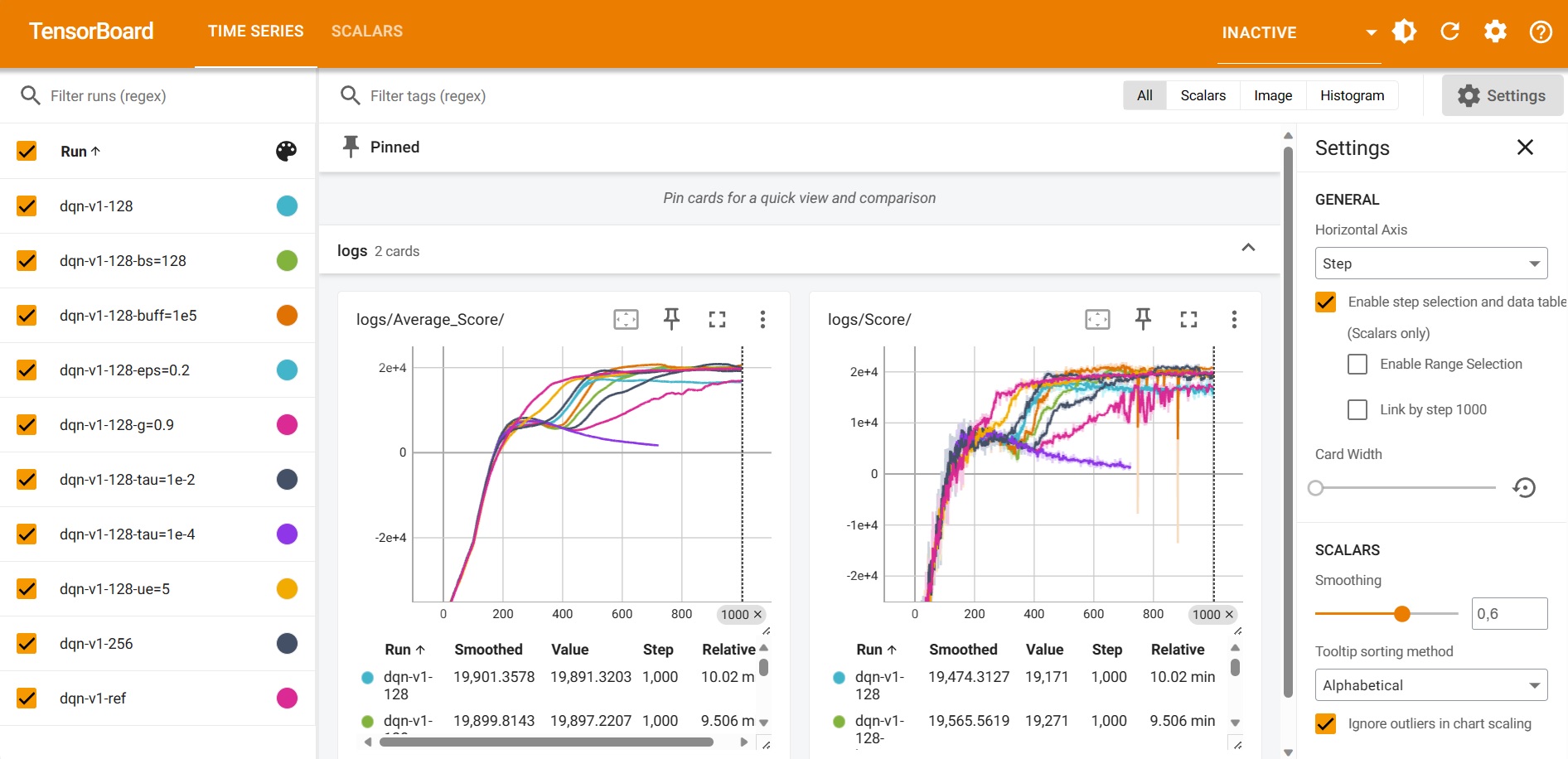
Training the DQN Model
from torch.utils.tensorboard import SummaryWriter
agent = Agent(state_dim=7,action_dim=21,seed=0)
def dqn(env, n_episodes= 1000, max_t = 10000, eps_start=1.0, eps_end = 0.01,
eps_decay=0.995):
"""Deep Q-Learning
Params
======
n_episodes (int): maximum number of training epsiodes
max_t (int): maximum number of timesteps per episode
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): mutiplicative factor (per episode) for decreasing epsilon
"""
#Tensorboard setup
writer=SummaryWriter(r"logs/dqn-v1-ref")
scores = [] # list containing score from each episode
eps = eps_start
for i_episode in range(1, n_episodes+1):
state = env.reset()
score = 0
for t in range(max_t):
action = agent.act(state,eps)
next_state,reward,done = env.step(action)
agent.step(state,action,reward,next_state,done)
state = next_state
score += reward
if done:
print('episode' + str(i_episode) + ':', score)
scores.append(score)
# Log the score to TensorBoard
writer.add_scalar(r"logs/Score/", score, i_episode)
# Log the average score over the last 100 episodes
avg_score = np.mean(scores[-100:])
writer.add_scalar(r"logs/Average_Score/", avg_score, i_episode)
break
eps = max(eps*eps_decay,eps_end)## decrease the epsilon
return scores
env = InvOptEnv(demand_hist)
scores= dqn(env)
Optimizing the (s, S) Policy
Both s and S are discrete values meaning there is a limited number of possible (s, S) policy combinations. We can use a brute force method to find the optimal (s, S) policy by iterating through all possible combinations and find the one that maximizes the profit.
However, this method is computationally expensive and not scalable. Hence, we will use a heuristic method to find the optimal (s, S) policy.
def profit_calculation_sS(s, S, demand_records):
total_profit = 0 # Initialize the total profit
inv_level = 25 # inventory on hand, use this to calculate inventory costs
lead_time = 2
capacity = 50 # Maximum inventory capacity
holding_cost = 3 # holding cost per unit per night
fixed_order_cost = 50 # fixed ordering cost per order
variable_order_cost = 10 # variable ordering cost per unit
unit_price = 30 # selling price per unit
order_arrival_list = [] # list of orders that are arriving in the future
for current_period in range(len(demand_records)):
inv_pos = inv_level # inventory position, use this to determine whether to order
if len(order_arrival_list) > 0: # if there is an order in the list
for i in range(len(order_arrival_list)): # for each order in the list
inv_pos += order_arrival_list[i][1] # update the inventory position
if inv_pos <= s: # if the inventory position is less than or equal to s
order_quantity = min(20,S-inv_pos) # order up to S units, with maximum of 20 units (maximum order capacity)
order_arrival_list.append([current_period+lead_time, order_quantity]) # add the order to the list
y = 1
else:
order_quantity = 0
y = 0
if len(order_arrival_list) > 0:
if current_period == order_arrival_list[0][0]:
inv_level = min(capacity, inv_level + order_arrival_list[0][1])
order_arrival_list.pop(0)
demand = demand_records[current_period]
units_sold = demand if demand <= inv_level else inv_level
profit = units_sold*unit_price-holding_cost*inv_level-y*fixed_order_cost-order_quantity*variable_order_cost
inv_level = max(0,inv_level-demand)
total_profit += profit
return total_profit
s_S_list = []
for S in range(1,61): # give a little room to allow S to exceed the capacity, should be calculated using safety stock
for s in range(0,S):
s_S_list.append([s,S])
profit_sS_list = []
for sS in s_S_list:
profit_sS_list.append(profit_calculation_sS(sS[0],sS[1],demand_hist))
best_sS_profit = np.max(profit_sS_list)
best_sS = s_S_list[np.argmax(profit_sS_list)]
Evaluating the model on test data
demand_test = []
for k in range(100,200):
np.random.seed(k)
demand_future = []
for i in range(52):
for j in range(4):
random_demand = np.random.normal(3, 1.5)
if random_demand < 0:
random_demand = 0
random_demand = np.round(random_demand)
demand_future.append(random_demand)
random_demand = np.random.normal(6, 1)
if random_demand < 0:
random_demand = 0
random_demand = np.round(random_demand)
demand_future.append(random_demand)
for j in range(2):
random_demand = np.random.normal(12, 2)
if random_demand < 0:
random_demand = 0
random_demand = np.round(random_demand)
demand_future.append(random_demand)
demand_test.append(demand_future)
The results show that in 100 different scenarios of a year’s worth of demand data, our agent that has been trained with Deep Q-Network performs better than the classic (s, S) Policy
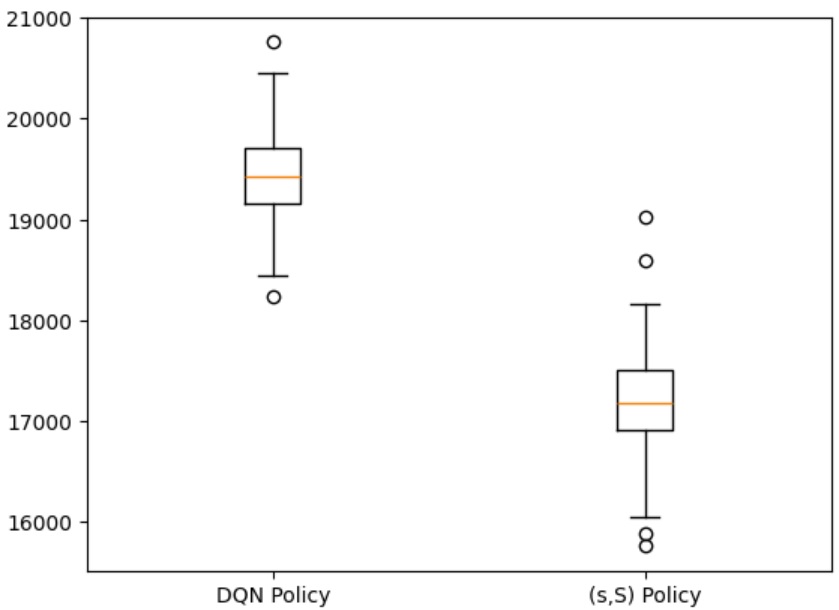
Now, let’s dive even deeper towards the specific actions that the agent took differently compared to the (s, S) policy.
This project is heavily inspired by the post made by Guangrui Xie, check it out here!